Une projection cartographique est une transformation systématique des latitudes et longitudes des lieux sur la surface d’une sphère ( ou presque comme la Terre ) dans des emplacements sur un plan pour réaliser une carte. Toutes les projections cartographiques déforment la surface d’une certaine façon. Selon le but de la carte, certaines distorsions sont acceptables et d’autres pas, donc différentes projections cartographiques existent afin de préserver certaines propriétés de la sphère au détriment d’autres propriétés.
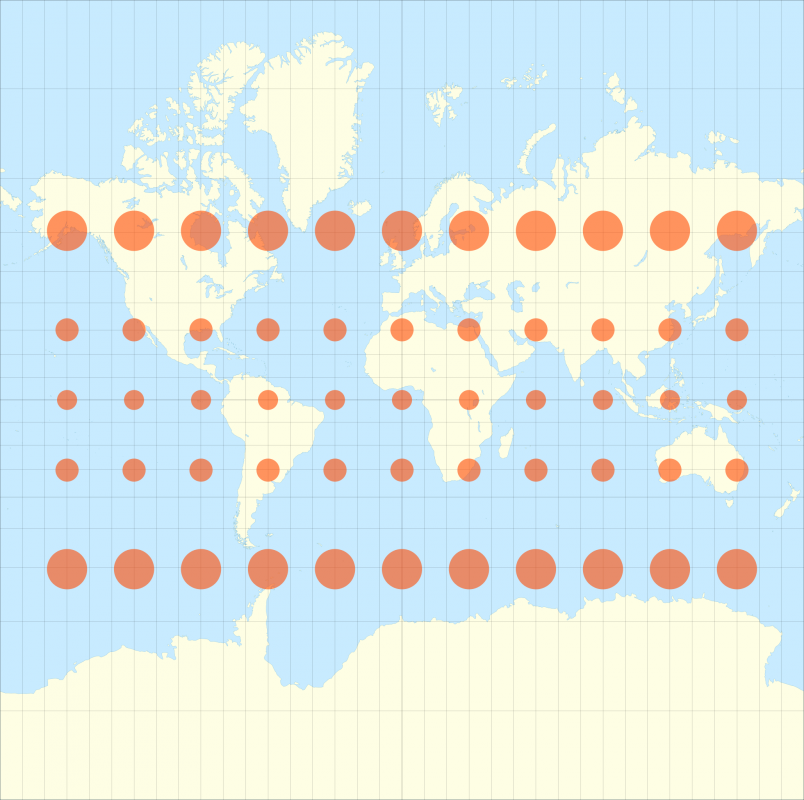
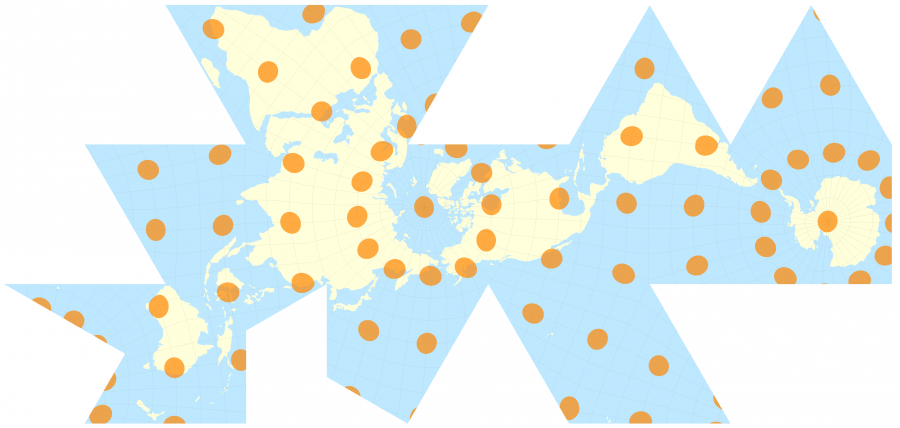
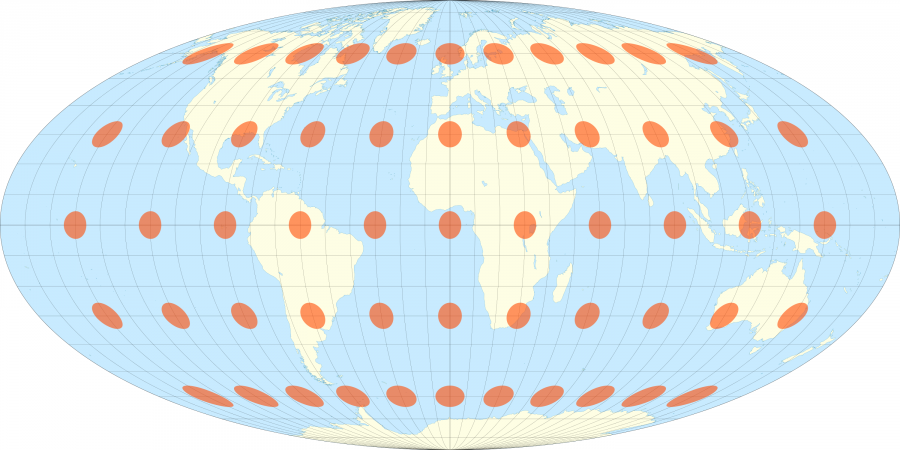
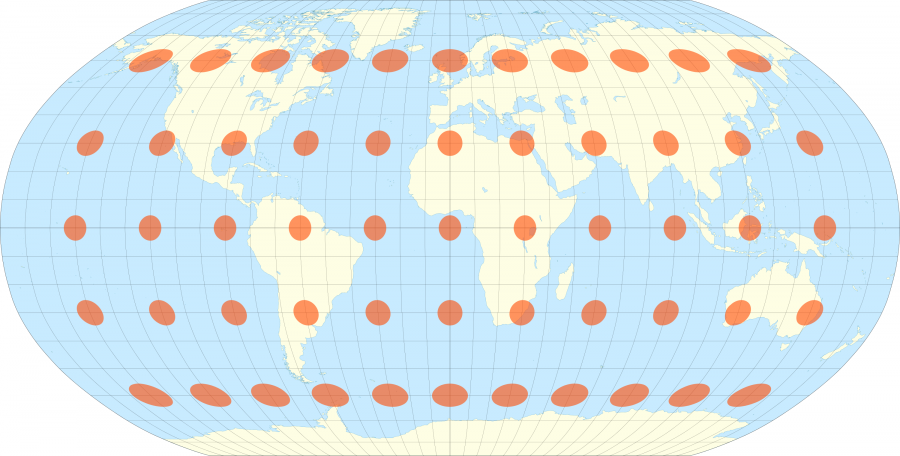
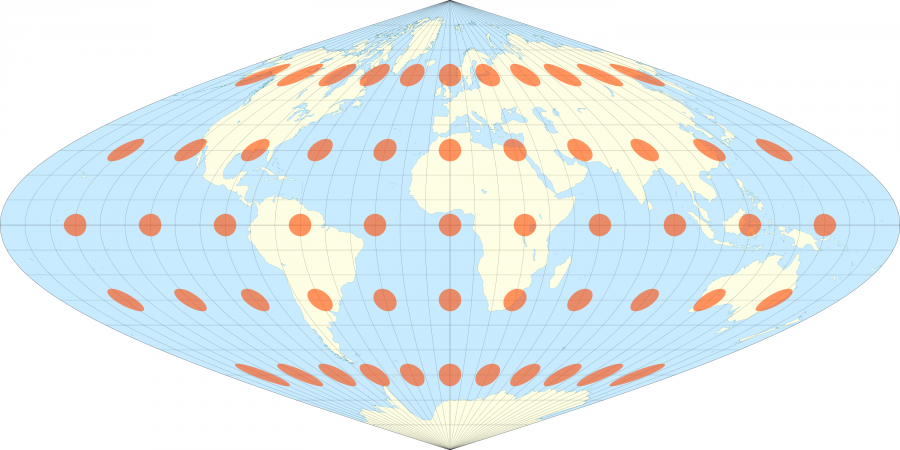
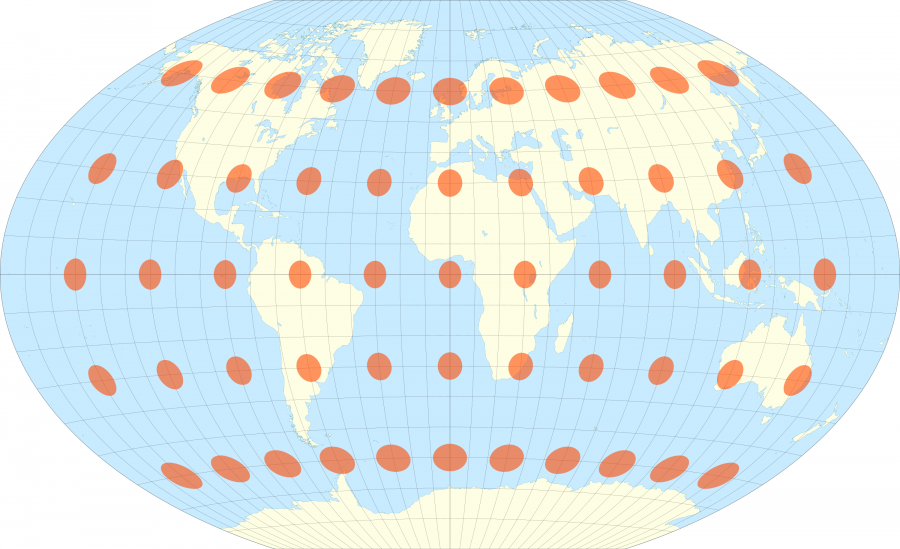
Le cartographe français Nicolas Auguste Tissot a inventé en 1851 un système étonnamment simple pour visualiser ces déformations. Son idée a été de placer sur les cartes des cercles espacés régulièrement auxquels sont appliqués les même déformations que celle que subissent la carte, se transformant en ovales et leurs rayons devenant plus important lorsque la projection donne plus d’importance à une région.
Sur toutes ces cartes les ovales oranges sont en réalité sur la surface de la Terre des cercles parfaits faisant tous 500km de rayon.
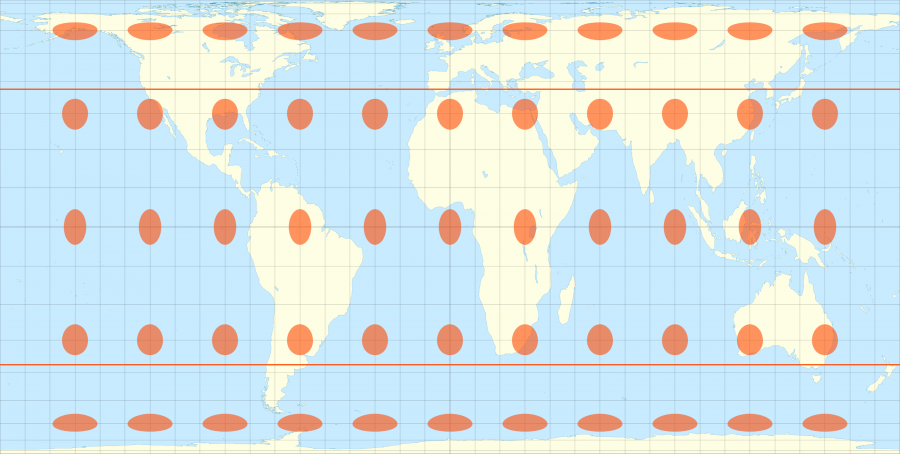
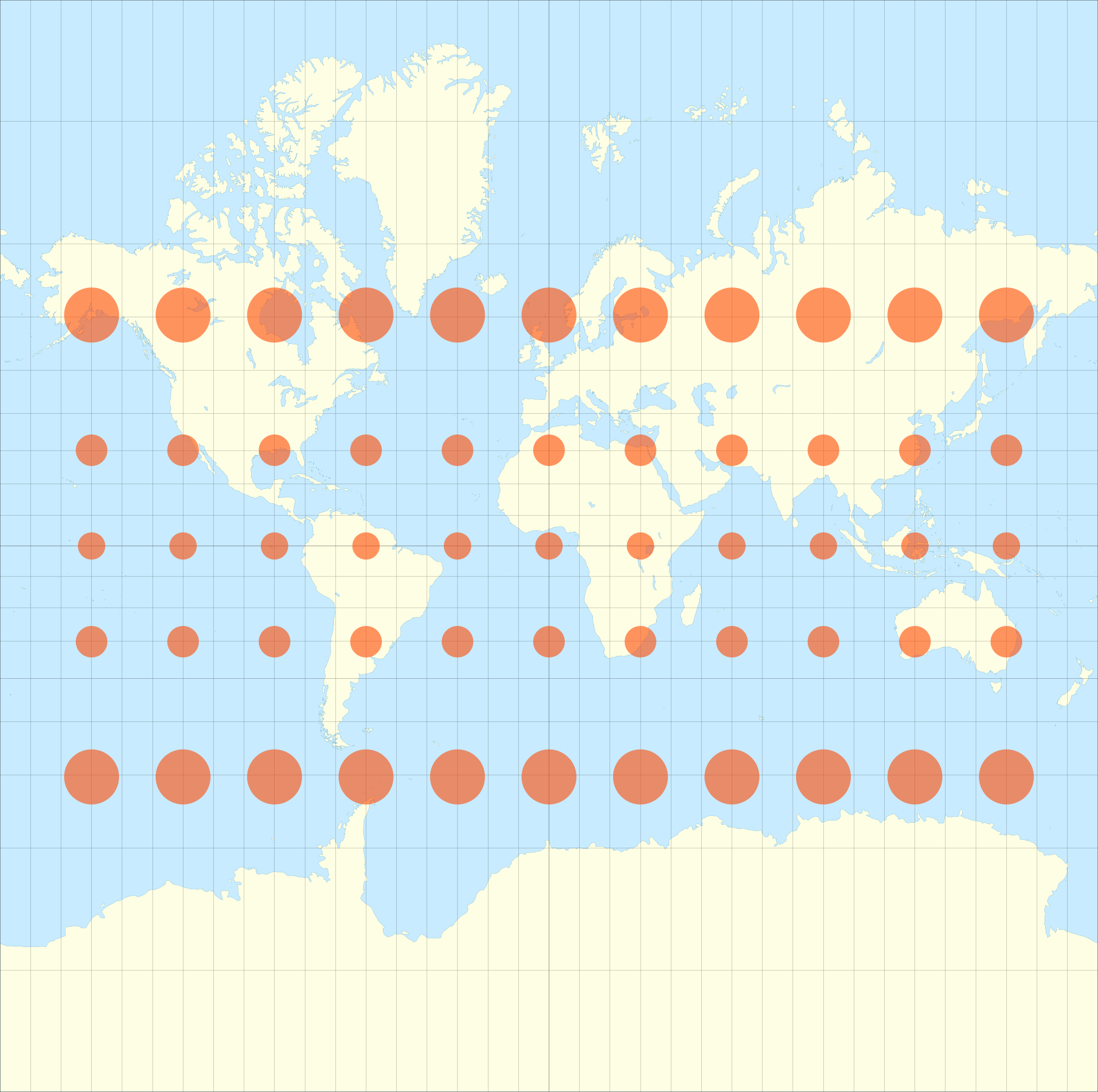
Sur la projection cylindrique de Mercator au dessus, une des plus utilisée, on voit parfaitement bien avec les indicatrices de Tissot à quel point elle donne plus d’importance aux zones près des pôles au détriment de celles proche de l’équateur. Par exemple l’Alaska et le Brésil semblent avoir la même taille sur la carte alors qu’en réalité le Brésil est 5 fois plus grand, ce qui est confirmé par les indicatrices de Tissot.
Par contre l’avantage de cette projection est de conserver les angles, les cercles restent donc bien ronds partout.
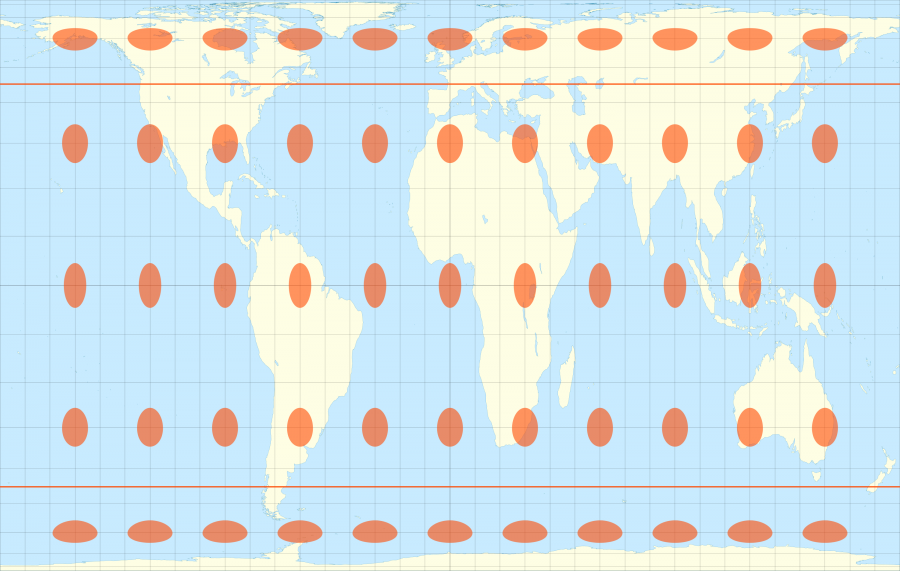
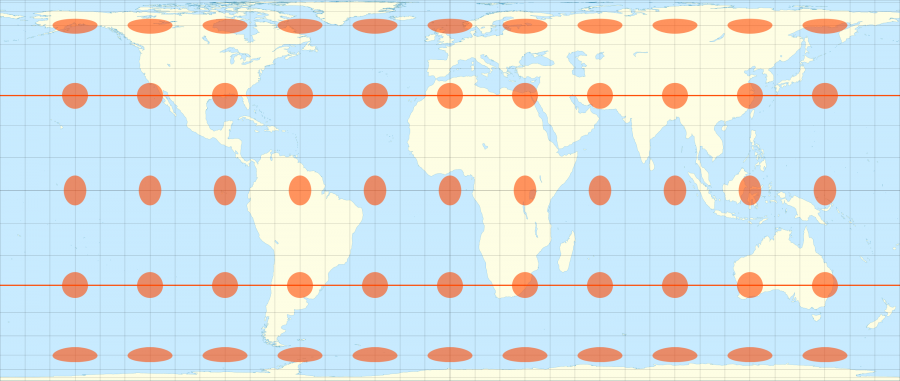
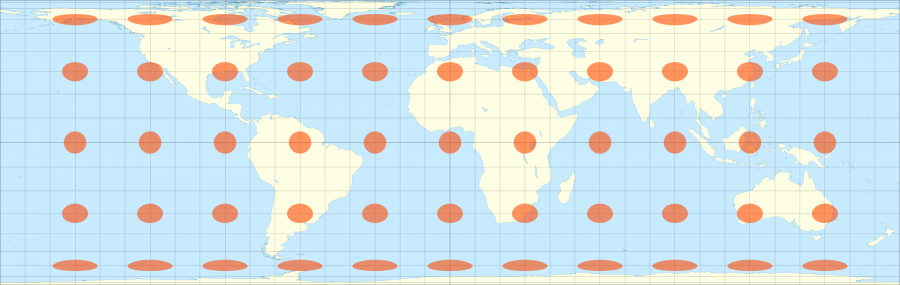
A l’inverse la projection de Peters en dessous conserve les proportions entre la taille des surfaces réelles et celles de la carte, au détriment de la forme réelle des continents, ce que les indicatrices de Tissot permettent bien de visualiser en ayants toutes la même taille mais en étant déformées suivant leurs position.
Vous devez être connecté pour poster un commentaire.